Hacking Shadows with 0x5F3759DF - Fast inverse square Root with magic numbers
Ideas from the Deep (id Software) #
In this short episode, I would like to pay tribute to one of the most remarkable software companies in the gaming industry of all time - id Software - creators of Doom, Quake, and many more.
Having recently read David Kushner's "Masters of Doom" during a holiday trip, my awe for their games and the impact of the two Johns (Carmack and Romero) on the field of 3D graphics and gaming in general re-emerged.
In this article, I would like to showcase one of the most brilliant yet simple (if understood) pieces of code I have ever encountered (see below).
While I would enjoy being able to clearly attribute the code to John Carmack, there is no official clarification of its journey into Quakes source code, although there are definitely rumours. Let's stick to the facts – John Carmack has accomplished other things that may be discussed in future blog posts.
But what is this Q_rqsrt all about? #
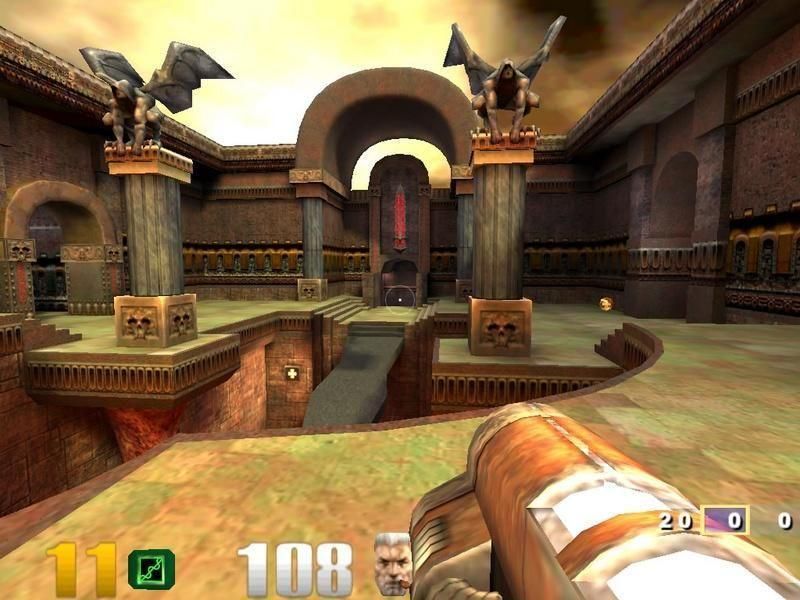
The Code calculates the inverse square root of a given float, estimating it cleverly as an optimization. This functionality is then used for shader compilation, which heavily relies on inverse square roots. The fast inverse square root enables the visual fidelity seen in the screenshot below (keep in mind, this is 1999 we are talking about).
Overcoming Hardware contemporary Hardware Limitations by Cheating Physics #
In today's world, games are often unoptimized, causing unnecessary hardware requirements and slow performance, if not both simultaneously[3].
This is in stark contrast to the late 90s, when hardware technology was the limiting factor affecting the ever-growing demand for more visual fidelity.
During that time, optimizing games heavily was the only way to ensure they ran as intended.
Now that the expectations have been set, let's examine the code and explore what enabled the shader calculations for Quake.
Excerpt from Quake III Arenas original Code:
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}The comments are original and taken straight from source [2]
The essence of the function is to compute a direct approximation utilizing the IEE754 structure of floats. Firstly, the method considers the 32-bit floating point word (y) as an integer (i). Next, the integer (i) is subtracted from the constant, and bitshifted against 1. Upon reinterpretation of this number as a float again (y), an initial rough estimation is obtained. One iteration of Newton's method is used to refine this result. The implementation is complete as the second iteration is not worth calculating, and is thus commented out.
What is noteworthy is that this technique is considerably slower than the SSE rsqrtss instruction, which was incorporated in processors launched in the same year. While the hardware did eventually keep pace (Moore's Law was still alive and well), it did so too late - thankfully, I might add.
[1] - Quake III Arena, Steam
[2] - Quake III Arena, id Software
[3] - PC gamers are getting really, really fed up with one sh*tty port after another, PC-Gamer
[4] - TIMING SQUARE ROOT, SOME ASSEMBLY REQUIRED